Question

Need help with this question please! The second drop down box options are quotientdifferenceproductsum

Answer 1

In order to solve this question, let's remember the meaning of the logarithm function:

If logₐb equals n, it means that aⁿ = b.

In other words, we need to find out which number that we can use as an exponent for a, such that the resulting power equals b.

Now, we can understand the following property of the logarithm function:

`\log _a(b)/(c)=\log _ab-\log _ac`

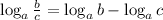
Let's see why this holds:

if we write b and c as powers of a, let's say

`\begin{gathered} b=a^x \\ \\ c=a^y \end{gathered}`

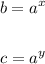
Then, we have:

`(b)/(c)=(a^x)/(a^y)=a^(x-y)`

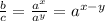
So:

`\log _a(b)/(c)=n\text{ }\Rightarrow\text{ }a^n=(b)/(c)\text{ }\Rightarrow a^n=a^(x-y)\text{ }\Rightarrow\text{ }n=x-y`

Therefore, the answer to the first box is:

`\log _bM-\log _bN`

And we concluded that the logarithm of a quotient is the difference of the logariths.

THus