Question

The Cadet is a popular model of sport utility vehicle, known for its relatively high resale value. The bivariate data given below were taken from a sample of sixteen Cadets, each bought new two years ago, and each sold used within the past month. For each Cadet in the sample, we have listed both the mileage x (in thousands of miles) that the Cadet had on its odometer at the time it was sold used and the price y (in thousands of dollars) at which the cadet was sold used. The least-squares regression line for these data has equation = 41.86-0.50x. This line is shown in the scatter plot below.

Answer 1

a)

The first answer is less than. This comes from the fact that the the regression line is decreasing, that means that for more mileage the selling price is decreasing.

b)

To find the decreased in price we use the regression equation:

`y=41.86-0.50x`

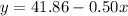
Now we just use two values for x. If x=0, the price is:

`y=41.86`

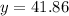
if x=1 then the the price is:

`y=41.36`

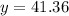
Therefore the difference in price is:

`0.5`

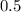
remember that this is given in thousands of dollar, therefore the difference in price is $500 for each thousand miles.