Question

[Honors] Two charged objects with an equal charge of Q separated by a distance r attract each other with a certain force. If the charges on both objects are doubled and the separation is halved, the force between them?(A) 4 times greater (B) 2 times greater (C) 4 times less(D) 16 times greater

Answer 1

The formula for force between charge particles is.

`\begin{gathered} F=k(q1q2)/(r^2) \\ Where,\text{ } \\ K=Constant=9*10^9(Nm^2)/(C^2) \\ q1=charge \\ q2=charge \\ r=distance\text{ }between\text{ }charge\text{ }paritlces \end{gathered}`

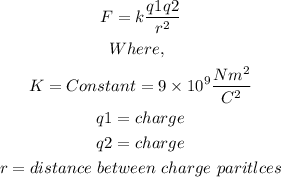
When charges are r distance apart then force between them is,

`F=K(Q^2)/(r^2)`

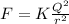
When charges are doubled and separation is halved then the new force between them is,

`F^(\prime)=K((2Q)(2Q))/(((r)/(2))^2)=K(4Q^2)/(((r^2)/(4)))=K(16Q^2)/(r^2)=16F`

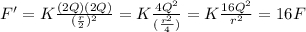
So the new force between them is 16 times greater as compare to before.

So option D is correct option.