From the question;
we are given the function
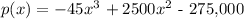
where
p(x) = profit
x = cost of advertising
we are to find the smallest of the two advertising amounts that produce a profit of $800,000.
this implies
p(x) = $800, 000
Therefore we have
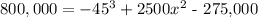
by simplifying the equation we get
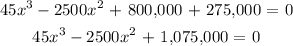
solving the equation using a calculator
we get the values of x to be
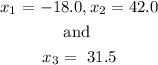
Since cost cannot be negative,
then the real solutions are
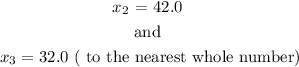
Therefore,
The smaller of the two advertising amounts that produce a profit of $800,000 is
x = 32