R)
Given the function of the height of the object, we can obtain its maximum by using its derivative, as shown below.
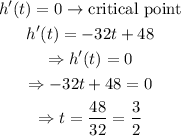
Then, the object will reach its maximum height at t=3/2, which is
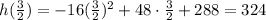
The time it takes for the object to reach its maximum height is 1.5 seconds.
The maximum height is 324 ft.