Question

A constant function has the form f(x) = c and has the domain of all real numbers with a range consisting of a single real number c.

Answer 1

The domain of a function f(x) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes.

A constant function is a linear function whose range contains only one element irrespective of the number of elements of the domain.

Since a constant function is defined for all real values of x, then we have that:

1) Its domain is the set of all real numbers, and

2) Since a constant function f(x) = c leads to only one output, which is k, its range is the set with just one element c.

Therefore,

`\begin{gathered} domain=\mathfrak{\Re } \\ range=c \end{gathered}`

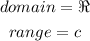
The statement is TRUE.