Given,
The mass of the hoover ball, m₁=0.35 kg
The velocity of the hoover ball before the collision, u=11 m/s
The mass of the hair/gumball, m₂=0.45 kg
The direction in which the hoover/hair/gumball goes after the collision, θ=32°
Let us assume that the eastward direction represents the positive x-axis and the northward direction represents the positive y-axis.
According to the law of conservation of momentum, the momentum is conserved in x and y directions separately and simultaneously.
Thus,
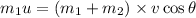
Where v is the velocity of the hoover/hair/gumball after the collision.
On substituting the known values,
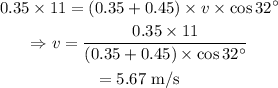
Thus the resultant velocity of the hoover/hair/gumball after the collision is 5.67 m/s.