We are given the function
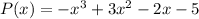
we are to use remainders theorem to find p(3)
Therefore
Given p(3) then x = 3
Hence
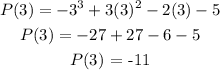
Hence, p(3) = - 11
Therefore, the Remainder is - 11
Finding the quotient
Given
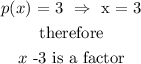
Therefore to find the quotient we will use long division method
![x-3\sqrt[]{-x^3+3x^(^2)-2x-5}](https://img.qammunity.org/2023/formulas/mathematics/high-school/6exopqphgmxetvhi5se3ukzn1tj0wj4lhi.png)
This gives
![\begin{gathered} \text{ -x}^2\text{ -2} \\ x-3\sqrt[]{-x^3+3x^2-2x-5} \\ \text{ (-) -}x^3+3x^2 \\ ----------------------- \\ \text{ -2x - 5 } \\ \text{ ( - ) -2x}^{}\text{ + 6} \\ -------------------- \\ \text{ - 11} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/r2oydics3i2szbjpocov53k3ydeimepgvc.png)
Therefore, The quotient is
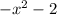
From the solution above
P(3) = - 11