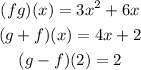Question

Suppose that the functions f and g are defined for all real numbers x as follows.f(x)=x+2g(x)=3x?Write the expressions for (&f)(x) and (g+f)(x) and evaluate (g-f)(2).(8-1)(x) = 0(8 +5)(x) = 0(8-5)(2) = 0=Х5?

Answer 1

Given:

`\begin{gathered} f(x)=x+2 \\ g(x)=3x \end{gathered}`

Required:

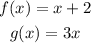
`\begin{gathered} (fg)(x)=? \\ (g+f)(x)=? \\ (g-f)(2)=? \end{gathered}`

Step-by-step explanation:

The algebraic operations of function f(x) and g(x) is given as

`(g+f)(x)=g(x)+f(x)`

Substituting the value of the functions in the above equation we get

`\begin{gathered} (g+f)(x)=g(x)+f(x) \\ (g+f)(x)=3x+x+2 \\ (g+f)(x)=4x+2 \end{gathered}`

Now algebraic operation for (f g)(x), we get

`(fg)(x)=f(x)g(x)`

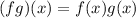
Substituting the values of function we get

`\begin{gathered} (fg)(x)=f(x)g(x) \\ (fg)(x)=(x+2)(3x) \\ (fg)(x)=3x^2+6x \end{gathered}`

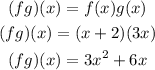
To find (g-f)(2), we first need to find (g-f)(x), which is given by

`(g-f)(x)=g(x)-f(x)`

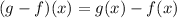
Substituting the values of function we get

`\begin{gathered} (g-f)(x)=g(x)-f(x) \\ (g-f)(x)=3x-(x+2) \\ (g-f)(x)=3x-x-2 \\ (g-f)(x)=2x-2 \end{gathered}`

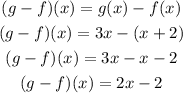
Now lets find (g-f)(2), for this substitute x = 2 in the above equation, we get

`\begin{gathered} (g-f)(x)=2x-2 \\ (g-f)(2)=2(2)-2=4-2 \\ (g-f)(x)=2 \end{gathered}`

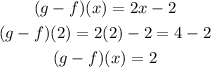
Final answer:

`\begin{gathered} (fg)(x)=3x^2+6x \\ (g+f)(x)=4x+2 \\ (g-f)(2)=2 \end{gathered}`