Question

A novelty clock has a 0.0200 kg mass object bouncing on a spring that has a force constant of 1.20 N/m.(a) What is the maximum velocity of the object in m/s if the object bounces 3.05 cm above and below its equilibrium position? (Enter the magnitude.) m/s(b) How many joules of kinetic energy does the object have at its maximum velocity? J

Answer 1

(a)

The maximum amplitude of the movement is 3.05 cm, which is 0.0305 meters.

Using this amplitude, we can find the total mechanical energy of the system (when the amplitude is maximum, the velocity is zero):

`\begin{gathered} ME=KE+PE\\ \\ ME=0+(kA^2)/(2)\\ \\ ME=0+(1.2\cdot0.0305^2)/(2)\\ \\ ME=0.00055815\text{ J} \end{gathered}`

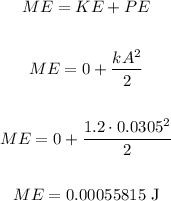
Now, let's use this energy to find the maximum velocity (when the velocity is maxed, the displacement is zero, the object is on the equilibrium position):

`\begin{gathered} ME=KE+PE\\ \\ 0.00055815=(mv^2)/(2)+0\\ \\ mv^2=0.0011163\\ \\ 0.02v^2=0.0011163\\ \\ v^2=0.055815\\ \\ v=0.236\text{ m/s} \end{gathered}`

The maximum velocity is 0.236 m/s.

(b)

When the object has maximum velocity, the kinetic energy is equal to the total mechanical energy of the system, which is 0.00055815 J.