We are asked to determine the graph of a function that is neither even nor odd. To do that let's remember how the graphs of even and odd functions are.
Even functions are functions that are symmetrical with respect to the y-axis. For example, the graph of:
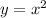
is the following:
Odd functions are functions that are symmetrical with respect to the origin. For example, the function:
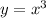
has the following graph:
Now, a function that is neither odd nor even must not have any of these two properties.
For example, the function:

The graph of this function is:
This graph has no symmetry with respect to the y-axis or the origin, therefore, is neither even nor odd.
Another example of a function that is neither odd nor even would be:
![y=\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/z3kevgn2c29nk34ba6n3a5xhvm9rhyzg0b.png)
The graph of this function is:
We notice that there is no symmetry with respect to the y axis or the origin, therefore, this graph is neither even nor odd.