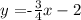1 Answer

Rafak · Answer 1 · 2023-09-09T18:38:33+0000

Solution:

Let us denote by L1 the line given by the following equation:

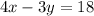
solving for 3y, this equation is equivalent to:

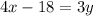
that is:

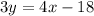
now, solving for y, we obtain:

that is:

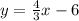
now, perpendicular lines have opposite-reciprocal slopes, so the slope of the line we want to find is

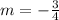
with this information, we can say that the provisional slope-intercept form of the perpendicular line to L1 is:

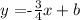
$y\text{ =-}(3)/(4)x+b$

our goal is now to find the y-intercept b of this line. To do this, we can replace the point (x,y)=(8, -8) into the previous equation, to get:

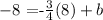
$-8\text{ =-}(3)/(4)(8)+b$

solving for b, we get:

so that, we can conclude that the equation of the line would be:

$y\text{ =-}(3)/(4)x-2$

Please log in or register to add a comment.