Question

An aluminum beam is 10.0 m long at a temperature of 25.0 °C. After heating, the final length of the beam is 10.012 m. What was the final temperature of the beam, if aluminum has a coefficient of linear expansion of 2.40 E -5 °C−1?150 °C75.0 °C100 °C125 °C

Answer 1

Given:

The length of the aluminum beam, L=10.0 m

The initial temperature, T₁=25.0 °C

The final length of the beam, l=10.0.12 m

The coefficient of linear expansion, α=2.40×10⁻⁵/°C

To find:

The final temperature of the beam.

Step-by-step explanation:

The coefficient of linear expansion is given by,

`\begin{gathered} \alpha=(\Delta L)/(L\Delta T) \\ =((l-L))/(L*\Delta T) \end{gathered}`

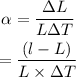
On substituting the known values,

`\begin{gathered} 2.40*10^5=((10.012-10))/(10*\Delta T) \\ \Rightarrow\Delta T=((10.012-10))/(10*2.40*10^(-5)) \\ =50\text{ }\degree C \end{gathered}`

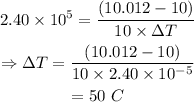
The change in the temperature is given by,

`\Delta T=T_2-T_1`

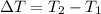
Where T₂ is the final temperature of the beam.

On substituting the known values,

`\begin{gathered} 50=T_2-25.0 \\ \Rightarrow T_2=50+25 \\ =75.0\text{ }\degree C \end{gathered}`

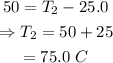
Final answer:

The final temperature of the beam is 75.0 °C