Question

4. A 30-60-90 triangle has a hypotenuse of 16 and a short side of 8. Use special right angle formulas to find the third side. Explain your work. Does your answer match what you got on number 3?

Answer 1

We are given the following right triangle:

The diagram shows a right triangle with a hypotenuse of 16 and a shorter side of 8. The angles are 30 -60 - 90. The shorter side is in front of the smaller angle. We can use the Pythagorean theorem to determine the length of the missing side:

`h^2=a^2+b^2`

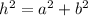
Where "h" is the hypotenuse, "a" and "b" are the sides. Substituting we get:

`16^2=8^2+x^2`

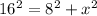
Now, we solve the squares:

`256=64+x^2`

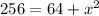
now, we subtract 64 from both sides:

`\begin{gathered} 256-64=x^2 \\ 192=x^2 \end{gathered}`

Now, we take the square root to both sides:

`\begin{gathered} √(192)=x \\ 13.86=x \end{gathered}`

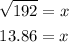
Therefore, the value of the missing side is 13.86