Question

Please help me with my math problems and explain each step clearly.

Answer 1

i.

Graphing the proportional relationship;

`y=1300x`

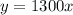
Note that the y-axis represents the amount of water in gal and the x-axis represents the time in hours.

ii.

The second city pool fills at a faster rate than the first city pool.

`\begin{gathered} r=1300\text{ gallons/hour} \\ r_2=3600\text{ gallons/hour} \end{gathered}`

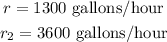
Step-by-step explanation:

i.

Given that the first pool is refilled at 5,200 gallons of water in 4 hours.

The rate of refilling the first pool is;

`\begin{gathered} r=(5200)/(4)\text{ gallons/hour} \\ r=1300\text{ gallons/hour} \end{gathered}`

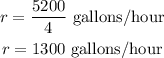
Graphing the proportional relationship;

`y=1300x`

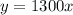
Note that the y-axis represents the amount of water in gal and the x-axis represents the time in hours.

ii

The second city pool as shown on the graph fills 10,800 gallons in 3 hours.

The rate of refilling the second city pool is;

`\begin{gathered} r_2=(10800)/(3)\text{ gallons/hour} \\ r_2=3600\text{ gallons/hour} \end{gathered}`

From the rate of refilling for the second city pool and the first city pool;

`\begin{gathered} r=1300\text{ gallons/hour} \\ r_2=3600\text{ gallons/hour} \end{gathered}`

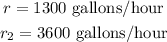
We can observe that the rate of refilling for the second city pool is higher than that of the first city pool.

Therefore, the second city pool fills at a faster rate than the first city pool.