a) Size of Angle AÖB = 45°
b) area of the shaded region is 31.2 cm²
Step-by-step explanation:
a) The radius = 10cm
∠AOB = θ
octagon has 8 sides, n = 8
Each of the triangles meet at a point.
The sum of angles at a point = 360°
Number of triangles in the octagon = 8
Each angle in the triangle = sum of angles at a point / number of triangles
Each angle = 360/8
Each angle = 45°
Size of Angle AÖB = 45°
b) The area of the shaded region = Area of circle - area of the octagon
To get area of the octagon, first we need to find area of the traingles. Since the triangles are equal, we will only find one of the area then multiply by number of triangles.
When we have two sides and an included angle, the area applied is:
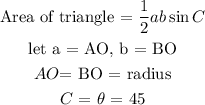
![\begin{gathered} \text{Area of triangle = }(1)/(2)*10\operatorname{cm}*10\operatorname{cm}*\sin 45 \\ \text{Area of triangle = }5\operatorname{cm}\text{ }*10\operatorname{cm}*0.7071 \\ \text{Area of triangle = 35.355 cm}^2 \end{gathered}]()
Area of the octagon = 35.355 cm² × 8 number of sides
Area of the octagon = 282.84 cm²
Area of circle = πr²
let π = 3.14
Area of circle = 3.14 × 10²
Area of circle = 314 cm²
The area of the shaded region = Area of circle - area of the octagon
Area of shaded region = 314 cm² - 282.84 cm²
Area of shaded region = 31.16 cm²
To 3 significant figure, area of the shaded region is 31.2 cm²