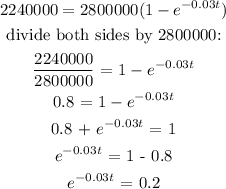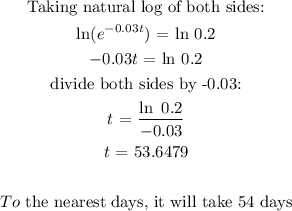Question

A lawyer has determined that the number of people p(t) in a city of 2.8 million people who have been exposed to a news item after t days is given by the function p(t)=2,800,000(1-e^-0.03t)(a) How many days after a major crime has been reported has 60% of the population heard of the crimes round your answer to the nearest day.(b) A defense lawyer knows it will be difficult to pick an unbiased jury after 80% of the population has heard of the crime. After how many days will 80% of the population have heard of the crime round your answer to the nearest day

Answer 1

a) it will take 31 days

b) it will take 54 days

Step-by-step explanation:

The number of people who have been exposed to a news item in a city after t days is given as:

`p\mleft(t\mright)=2,800,000\mleft(1-e^(-0.03t)\mright)`

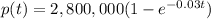
a) We need to find the number of days it took 60% of the population to hear the news

p(t) = 60% of the population

Total population = 2.8 million

p(t) = 60% × 2800000 = 1680000

t = ?

substitute the value of p(t) to get t:

`\begin{gathered} 1680000=2800000\mleft(1-e^(-0.03t)\mright) \\ \text{divide both sides by 2800000}\colon \\ \frac{1680000}{\text{2800000}}=1-e^(-0.03t) \\ 0.6\text{ = }1-e^(-0.03t) \\ 0.6\text{ - 1 = }-e^(-0.03t) \\ -0.4\text{ = }-e^(-0.03t) \\ \\ \text{divide both sides by -1:} \\ 0.4\text{ = }e^(-0.03t) \end{gathered}`
`\begin{gathered} \text{Taking natural log of both sides:} \\ \log _e0.4\text{ =}\log _e(\text{ }e^(-0.03t)) \\ \log _e0.4\text{ = -0.03t} \\ \ln \text{ 0.4 = -0.03t} \\ \\ \text{divide both sides by -0.03:} \\ \frac{\ln\text{ 0.4}}{\text{-0.03}}\text{ = t} \\ t\text{ = }30.5430\text{ } \\ \\ To\text{ the nearest day, it will take 31 days} \end{gathered}`

b) We need to find the number of days it took 80% of the population to hear the news

p(t) = 80% of the population = 80% (2800000)

p(t) = 2240000

substitute the value of p(t) into the formula:

`\begin{gathered} 2240000=2800000\mleft(1-e^(-0.03t)\mright) \\ \text{divide both sides by 2800000:} \\ (2240000)/(2800000)\text{ = }1-e^(-0.03t) \\ 0.8\text{ = }1-e^(-0.03t) \\ 0.8\text{ + }e^(-0.03t)\text{ = 1} \\ e^(-0.03t)\text{ = 1 - 0.8} \\ e^(-0.03t)\text{ = 0.2} \end{gathered}`
`\begin{gathered} \text{Taking natural log of both sides:} \\ \ln (e^(-0.03t))\text{ = ln 0.2} \\ -0.03t\text{ = ln 0.2} \\ \text{divide both sides by -0.03:} \\ t\text{ = }\frac{\ln \text{ 0.2}}{-0.03} \\ t\text{ = 53.6479} \\ \\ To\text{ the nearest days, it will take 54 days} \end{gathered}`