Question

A boat is travelling at 18 knots on a heading of 234 degrees. The current is 8 knots, flowing from a bearing of 124 degrees. Determine the resultant velocity of the boat and provide a diagram.

Answer 1

Boat original speed: 18 knots

Boat original direction: 234°

Current speed: 8 knots

Current direction: 124° + 180° = 304° (because it says "flowing from a bearing of 124°")

The diagram of the problem is as follows:

We can calculate the velocity of the boat and the current using the speed and the direction:

`\begin{gathered} \vec{v}_(boat)=(18\cos234\degree,18\sin234\degree)=(-10.5801,-14.5623) \\ \\ \vec{v}_(current)=(8\cos304\degree,8\sin304\degree)=(4.47354,-6.6323) \end{gathered}`

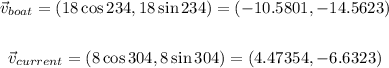
Finally, the resultant velocity for the boat is the vector sum between the original velocity of the boat and the velocity of the current:

`\begin{gathered} \vec{v}_(resultant)=\vec{v}_(boat)+\vec{v}_(current)=(-10.5801,-14.5623)+(4.47354,-6.6323) \\ \\ \therefore\vec{v}_(resultant)=(-6.107,-21.195)\text{ knots} \end{gathered}`

And the resultant speed is 22.057 knots