Question

Given g(x) =1/x^-3, Sketch the graph for g(x) and find the total area between the curve g(x) and x-axis. Explain if necessary and provide reason if the questions cannot be solved.

Answer 1

Given:

`g\mleft(x\mright)=(1)/(x^3)`

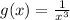
Required:

Sketch the graph for g(x) and find the total area between the curve g(x) and x-axis. Explain if necessary and provide a reason if the question cannot be solved.

Step-by-step explanation:

The given function is:

`g(x)=(1)/(x^(3))`

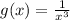
We can observe from the graph that there is no bounded area between the graph of the function and the x-axis.

To find the area between the x-axis and the curve the area should be bound with the x-axis.

So the area of the given function can not be calculated.

Final answer:

The question can not be solved because there is no bounded area between the graph of the function and the x-axis.