We have a sample that in fact represents the population.
We have to calculate the standard deviation of this population.
The difference between the standard deviation of a population comparing it to the calculation of the standard deviation of a sample is that we divide by the population side n instead of (n-1).
We have to start by calculating the mean of the population first:
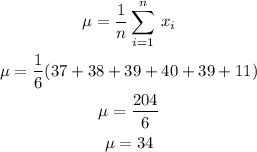
Now, we can calculate the standard deviation as:
![\sigma=\sqrt[]{(1)/(n)\sum^n_(i=1)\, (x_i-\mu)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/60sfdpv2iz8y6ya2mxg563dul3jligt7z4.png)
![\begin{gathered} \sigma=\sqrt[]{(1)/(6)((37-34)^2+(38-34)^2+(39-34)^2+(40-34)^2+(39-34)^2+(11-34)^2)} \\ \sigma=\sqrt[]{(1)/(6)(3^2+4^2+5^2+6^2+5^2+(-23)^2)} \\ \sigma=\sqrt[]{(1)/(6)(9+16+25+36+25+529)} \\ \sigma=\sqrt[]{(1)/(6)(640)} \\ \sigma\approx\sqrt[]{106.67} \\ \sigma\approx10.33 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ngkgkiosqbj93o5swmj5bbp6pt7owdqb0s.png)
Answer: the standard deviation of this population is approximately 10.33