Question

How many times greater is 3.8 x 10^5 than 3.8 x 10^-7?

Answer 1

`10^(12)`

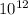
Step-by-step explanation

We want to find out how many times 3.8 x 10^5 is greater than 3.8 x 10^-7.

To do that, we have to divide 3.8 x 10^5 by 3.8 x 10^-7 and then find the answer.

Let us do that:

`\begin{gathered} (3.8\cdot10^5)/(3.8\cdot10^(-7))\text{ = }(3.8)/(3.8)\cdot\text{ }(10^5)/(10^(-7)) \\ U\sin g\text{ the division law of indices:} \\ 1\cdot(10^{5\text{ -(-7)}})=10^(5+7) \\ =10^(12) \end{gathered}`

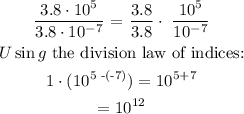
Note: The division law of indices states that if a numerator and a denominator have the same base (e.g. 10), then the power of the numerator can subtract of the denominator.

Therefore, 3.8 x 10^5 is greater than 3.8 x 10^-7 by 10^(12) times