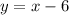Question

What is the linear equation of (10,4) (-4,-10)

Answer 1

In order to define a linear function, we can use its slope-intercept form shown below:

`y=mx+b`

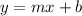
Then, to find the slope 'm' and the y-intercept 'b', we can use the two points given, that is, apply the x and y values of the point in the equation.

So we have:

`\begin{gathered} y=mx+b \\ (10,4)\colon \\ 4=10m+b \\ (-4,-10)\colon \\ -10=-4m+b \end{gathered}`

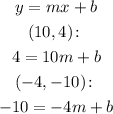
We can solve this system of equations by subtracting the first and second equation to find the value of m:

`\begin{gathered} 4-(-10)=10m+b-(-4m+b) \\ 4+10=10m+b+4m-b \\ 14=14m \\ m=1 \\ \\ 4=10m+b \\ 4=10+b \\ b=4-10 \\ b=-6 \end{gathered}`

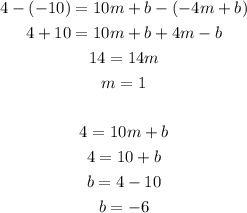
So our linear equation is:

`y=x-6`