Question

Determine the direction the parabola opens and the y-intercept for the function

Answer 1

`\begin{gathered} (a)\text{upwards } \\ (b)\text{y-intercept is -6} \end{gathered}`

Step-by-step explanation

Step 1

Given

`y=ax^2+bx+c`

If a > 0 (positive) then the parabola opens upward.

If a < 0 (negative) then the parabola opens downward.

Hence

`\begin{gathered} ax^2+bx+c\rightarrow3x^2+9x-6 \\ therefore \\ a=3 \end{gathered}`

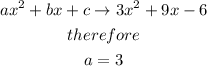
it means, the parabola opens upward

Step 2

x-intercept:

The y-intercept of any graph is a point on the y-axis and therefore has x-coordinate 0.

`\begin{gathered} y=3x^2+9x-6 \\ at\text{ x=0} \\ y=3(0)^2+9(0)-6 \\ y=-6 \\ so\text{, the y-intercept is -6} \end{gathered}`

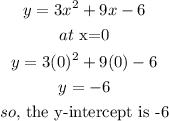
I hope this helps you

s