GIven:
The given points are (6,-6) and (8,-3).
The objective is to find the equation of the line in slope intercept form.
Consider the given points are,
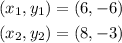
The general equation for straight line through two points is,
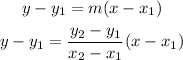
Here, m represents the slope of the equation.
On plugging the values in the above equation,
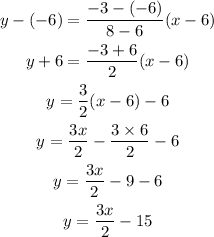
Hence, the equation of line in slope intercept form is y = (3/2)x-15.