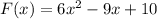Question

Find the particular antiderivative F(x) off(x) = 12x - 9 that satisfies F(1) = 7.

Answer 1

Given the question in the image, the following are the solution steps to get the answer

Step 1: Define antiderivative

Antiderivative of a function is nothing but integral with respect to x

`F(x)=\int f(x)dx`

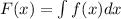
Step 2: Find the antiderivative of the given function in the question

`\begin{gathered} f(x)=12x-9 \\ F(x)=\int (12x-9)dx \\ \text{Providing integral to each term, we have} \\ F(x)=\int 12xdx-\int 9dx \\ F(x)=12\int xdx-9\int x^0dx---(1) \\ we\text{ know that} \\ \int x^ndx=\frac{x^{^(n+1)^{}}}{n+1},n\\e1 \\ F(x)=12*(x^(1+1))/(1+1)-9*(x^(0+1))/(0+1)+c \\ F(x)=12*(x^2)/(2)-9*(x)/(1)+c \\ F(x)=6x^2-9x+c----(2) \end{gathered}`

Step 3: we find the value of c in front of the integration formula

`\begin{gathered} \text{Given that F(1)=7} \\ 6(1)^3-9(1)+c=7 \\ 6-9+c=7 \\ c=7-6+9 \\ c=10 \end{gathered}`

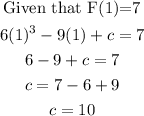
Step 4: We write the final result for F(x)

`\begin{gathered} \text{Hence, we have:} \\ F(x)=6x^2-9x+10 \end{gathered}`

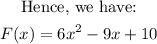
Hence, the final result for F(x) is given as:

`F(x)=6x^2-9x+10`