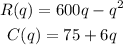
Total profit earned:
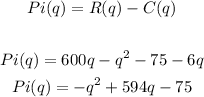
Profit Maximizing Quantity:
1-Determine marginal revenue by taking the derivative of total revenue

2-Determine marginal cost by taking the derivative of total cost
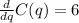
3-Set marginal revenue equal to marginal cost and solve for q

Then, the profit maximizing quantity is 297