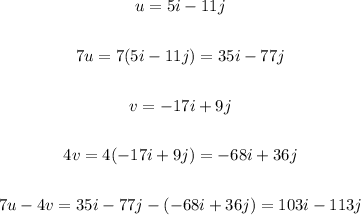Question

Hello! Would like help on parts b and c. Thanks!PART A:u = 5i - 11jv = -17i +9j

Answer 1

PART B:

To find the trigonometric form, we need the magnitude and angle of each vector.

The magnitude can be found with the expressions below:

`\begin{gathered} ||u||=√(a^2+b^2)=√(5^2+(-11)^2)=√(25+121)=√(146)=12.08\\ \\ ||v||=√(a^2+b^2)=√((-17)^2+9^2)=√(289+81)=√(370)=19.24 \end{gathered}`

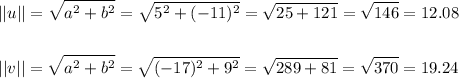
And the angle of each vector can be found with the expressions below:

`\begin{gathered} \theta_u=\tan^(-1)((b)/(a))=\tan^(-1)((-11)/(5))=294.44°\\ \\ \theta_v=\tan^(-1)((b)/(a))=\tan^(-1)((9)/(-17))=152.10° \end{gathered}`

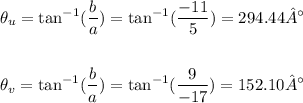
Therefore vectors u and v in the trigonometric form are:

`\begin{gathered} u=12.08(\cos294.44°i+\sin294.44°j)\\ \\ v=19.24(\cos152.10°i+\sin152.10°j) \end{gathered}`

PART C:

To find 7u - 4v, let's use the linear form of each vector, multiply by the constant values and subtract the results:

`\begin{gathered} u=5i-11j\\ \\ 7u=7(5i-11j)=35i-77j\\ \\ v=-17i+9j\\ \\ 4v=4(-17i+9j)=-68i+36j\\ \\ 7u-4v=35i-77j-(-68i+36j)=103i-113j \end{gathered}`