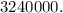Question

Each student at college has a student ID number consisting for four digits (the first digit is non zero and digits can repeat) followed by four letters A, B, C, D, E, and F (letters cannot repeat). How many different student numbers are possible?

Answer 1

First, we count the number of ways we can arrange the digits. The first number has 9 possibilities:

`1\text{ to 9,}`

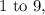
the other digits have 10 possibilities each:

`0\text{ to 10.}`

Therefore, the number of ways we can arrange the digits is:

`9*10*10*10=9*10^3=9000.`

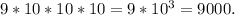
Now, for the letters, the order matters, therefore, we can use the permutation formula:

`P(6,4)=(6!)/((6-4)!)=360.`

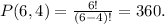
Finally, the total possible number of IDs is:

`9000*360=3240000.`

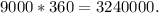
Answer:

`\begin{equation*} 3240000. \end{equation*}`