Question

Sketch an angle θ in standard position such that θ has the least positive measure and given point is on terminal side of θ.(-2,5)

Answer 1

Given that:

- The angle θ must be in Standard Position.

- The angle must have the least positive measure.

- The following point must be on the terminal side of the angle:

`\mleft(-2,5\mright)`

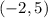
By definition, an angle in Standard Position is its vertex at the Origin and one of the rays (one of the sides of the angle) is located on the positive side of the x-axis.

Notice that the coordinates of the given points are:

`\begin{gathered} x=-2 \\ y=5 \end{gathered}`

Then, you can plot it on a Coordinate Plane:

Knowing the definition shown above, you can draw the initial side (which is on the positive x-axis). The terminal side must pass through the given point. See the picture below:

By definition, the measurement is positive when the angles are measured in counterclockwise direction. Knowing this, you can sketch the angle θ.

Hence, the answer is: