Solution:
Given the figure below:
The above figure, when closed, results into a cuboid.
This can be proven in the diagram below:
where the cuboid has
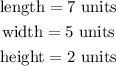
The surface area of a cuboid is expressed as
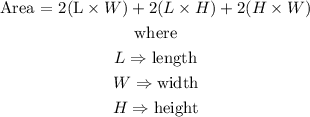
Thus, the surface area of the cuboid is evaluated as
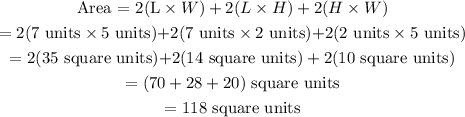
Hence, the surface area of the box is
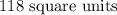
The correct option is D.