Question

Determine algebraically where the cubic polynomial function that has zeroes at 3,4, and -4 and passes through the point (2,24) has a value of 120.

Answer 1

Given the word problem, we can deduce the following information:

1. The function has zeroes at 3,4, and -4 and passes through the point (2,24) has a value of 120.

To determine the cubic polynomial function, we let the values of x be:

x=3

x=4

x=-4

Since we the polynomial function is cubic, it would be like this:

`P(x)=a(x-3)(x-4)(x-5)`

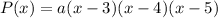
To determine a or the constant, we let P(x)=24 and x=2:

`\begin{gathered} P(x)=a(x-3)(x-4)(x-5) \\ 24=a(2-3)(2-4)(2-5) \\ 24=a(-1)(-2)(-3) \\ \text{Simplify and rearrange} \\ 24=a(-6) \\ a=(24)/(-6) \\ a=-4 \end{gathered}`

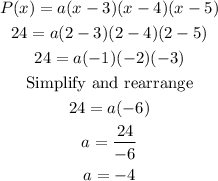
Next, we plug in P(x)=120 and a=-4 into P(x)=a(x-3)(x-4)(x-5):

`\begin{gathered} 120=-4(x-3)(x-4)(x-5) \\ \end{gathered}`

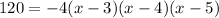
We can further simplify this into standard form. So,

`\begin{gathered} 120=-4(x-3)(x-4)(x-5) \\ 120=-4x^3+48x^2-188x+240 \\ -4x^3+48x^2-188x+120=0 \end{gathered}`

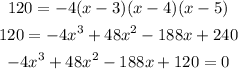
The graph would be:

The root or the x-intercept would be found at x=0.78553.

Therefore, the answer is x=0.78553.