First, to find the new function that will have a horinzontal stretch with a factor of 5, we just need to substitute the values of x in the function by x/5 (we divide by 5 because it is a stretch. If it was a compression, we would multiply by 5):
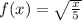
Then, to find the new function with a reflection in the y-axis, we just need to substitute the values of x by -x (the minus sign will cause a reflection in the y-axis):
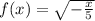
So the final function, starting from the function f(x) = √x, that will have a horizontal stretch with a factor of 5, followed by a reflection in the y-axis, is the function above.