Question

2(3x + 2) < – 2x – 12write the solution using interval notation

Answer 1

`(-\infty,-2)`

Explanation:

Given the below;

`2(3x+2)<-2x-12`

We'll follow the below steps to solve for x;

Step 1: Clear the parentheses on the left-hand side by expansion;

`6x+4<-2x-12`

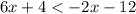
Step 2: Subtract 4 from both sides;

`\begin{gathered} 6x<-2x-12-4 \\ 6x<-2x-16 \end{gathered}`

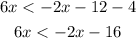
Step 3: Add 2x to both sides;

`\begin{gathered} 6x+2x<-16 \\ 8x<-16 \end{gathered}`

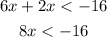
Step 4: Divide both sides by 8;

`\begin{gathered} (8x)/(8)<(-16)/(8) \\ x<-2 \end{gathered}`

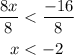
We can see from the above that the solution to the inequality are all values of x that are less than -2, so we can go ahead and write the solution using interval notation as seen below;

`(-\infty,-2)`