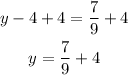Question

Write the equation of the line that passes through the points (0,4)and (-9, -3). Put your answer in fully reduced point-slope form,unless it is a vertical or horizontal line.

Answer 1

To determine the equation of the line you have to use the point-slope form

`y-y_1=m(x-x_1)`

Where

(x₁, y₁) are the coordinates of one point on the line

m is the slope

We know two points crossed by the line (0, 4) and (-9,-3), using them we can calulate the slope as:

`m=(y_1-y_2)/(x_1-x_2)`

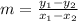
Where

(x₁, y₁) are the coordinates of one point on the line

(x₂, y₂) are the coordinates of a second point on the line

`\begin{gathered} m=(4-(-3))/(0-(-9)) \\ m=(4+3)/(9) \\ m=(7)/(9) \end{gathered}`

Now that we know the slope of the line, we can determine the equation using

m=7/9 and (0,4)

`\begin{gathered} y-4=(7)/(9)(x-0) \\ y-4=(7)/(9)x \end{gathered}`

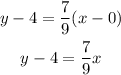
Pass "-4" to the other side of the equation to express the equation in slope-intercept form

`\begin{gathered} y-4+4=(7)/(9)+4 \\ y=(7)/(9)+4 \end{gathered}`