1 Answer

Ask a Question

Sumit Parakh · Answer 1 · 2023-08-29T02:31:07+0000

Given:

There are given that the cos function:

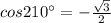
$cos210^(\circ)=-(√(3))/(2)$

Step-by-step explanation:

To find the value, first, we need to use the half-angle formula:

So,

From the half-angle formula:

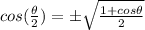
$cos((\theta)/(2))=\pm\sqrt{(1+cos\theta)/(2)}$

Then,

Since 105 degrees is the 2nd quadrant so cosine is negative

Then,

By the formula:

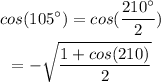
$\begin{gathered} cos(105^(\circ))=cos((210^(\circ))/(2)) \\ =-\sqrt{(1+cos(210))/(2)} \end{gathered}$

Then,

Put the value of cos210 degrees into the above function:

So,

$\begin{gathered} cos(105^(\circ))=-\sqrt{(1+cos(210))/(2)} \\ cos(105^{\operatorname{\circ}})=-\sqrt{(1-(√(3))/(2))/(2)} \\ cos(105^(\circ))=-\sqrt{(2-√(3))/(4)} \\ cos(105^(\circ))=-\frac{\sqrt{2-√(3)}}{2} \end{gathered}$

Final answer:

Hence, the value of the cos(105) is shown below:

$cos(105^{\operatorname{\circ}})=-\frac{\sqrt{2-√(3)}}{2}$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions