Question

A figure is dilated by a factor of 3. which statement about the measurements of the figure is true?A. the perimeter of the original figure is multiplied by 3 , and the area is multiplied by 9. B. the perimeter and area of the original figure are tripled. C. the perimeter of the original figure is multiplied by 9 and the area is multiplied by 27. D. the perimeter of the original figure is multiplied by 9 and the area is multiplied by 3.

Answer 1

A dilation is a transformation that modifies the shape of a figure by a determined scale factor.

• If the scale factor is less than one, ,k < 1,, then the transformation is a ,reduction ,and the resulting figure is smaller than the original.

,

• If the scale factor is greater than one, ,k > 1,, then the transformation is an ,enlargement ,and the resulting figure is greater than the original.

The image was dilated by a scale of factor 3, this factor is greater than 1, so the resulting image will be greater than the original one.

To enlarge the figure each side will be multiplied by 3.

The perimeter of a dilated figure is equal to the perimeter of the original figure multiplied by the scale factor.

`P_{\text{dilation}}=kP`

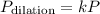
So the perimeter of the enlarged figure will be equal to the perimeter of the original figure multiplied by 3.

The area of a dilated figure is equal to the area of the original figure multiplied by the square of the scale factor.

`A_{\text{dilation}}=Ak^2`

So the area of the enlarged figure will be equal to the area of the original figure multiplied by the square of 3, i.e. multiplied by 9.

The correct option is A.