From the given graph, let's find the time it takes the projectile to reach its maximum height.
Given:
θ = 40 degrees
Initial velocity, vo = 250 m/s.
To find the time it takes the projectile to reach maximum height, apply the formula:
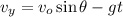
Where:
vy is the final velocity at maximum height = 0 m/s
vo is the initial velocity
g is acceleration due to gravity = 9.8 m/s²
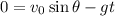
Rewrite the formula for the time, t:
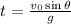
Input values into the formula and solve for t:
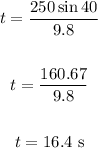
Therefore, the time it takes the projectile to reach its maximum height is 16.40 seconds.
ANSWER:
a. 16.40 s
a. 16.40