Let "θ" represent the angle whose measure we need to find.
Complement (c) of θ
If two angles are complementary, it means that their sum is equal to 90 degrees. To determine the measure of the complement of a given angle "θ", you have to calculate the difference between 90 and the said angle. You can express the value of the complement as:
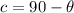
Supplement (s) of θ
Two angles are supplementary when their sum is equal to 180º. To determine the measure of the complement of a given angle "θ", you have to calculate the difference between 180º and the said angle. You can express the value of the supplement as follows:

For the angle "θ" we know that "twice the complement", symbolically 2c, is equal to "50 less than the angle's supplement", symbolically s-50.
So that:
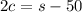
Replace the expressions obtained for c and s:

From this expression, we can determine the measure of the angle:
-First, distribute the multiplication on the left side of the expression, and simplify the like terms on the right side:
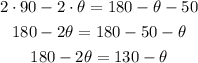
-Second, pass "180" to the right side of the equation by applying the opposite operation "-180" to both sides of it.
Use the same method to pass "-θ" to the left side of the equation:
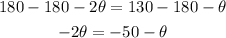
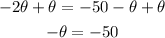
-Third, multiply both sides of the expression by -1 to reach the measure of θ
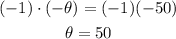
The measure of the angle is θ=50º