Given,
The mass attached to the spring, m=2 kg
The spring constant of the spring to which the mass is attached, k=200 N/m
The time of the oscillation of the oscillator is given by,
![T=2\pi\sqrt[]{(m)/(k)}](https://img.qammunity.org/2023/formulas/physics/high-school/59p5w267zpcbiffehn6l28fg1lc6criikc.png)
The frequency is related to the period of the oscillator as,
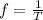
Thus the frequency of the oscillator is given by,
![f=(1)/(2\pi)\sqrt[]{(k)/(m)}](https://img.qammunity.org/2023/formulas/physics/college/d1stca0n17wrsw81f5wzjgx4jw1bwybjwt.png)
On substituting the known values in the above equation,
![\begin{gathered} f=(1)/(2\pi)\sqrt[]{(200)/(2)} \\ =1.59\text{ Hz} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/lka1n3fnmxl573vp5r1t092mmubonifjnl.png)
Thus the frequency of oscillation of thus formed oscillator is 1.59 Hz