SOLUTION
Given the question in the image, the following are the solution steps to answer the question
STEP 1: Define the FOIL method of multiplication
The FOIL Method is used to multiply binomials. FOIL F O I L is an acronym. The letters stand for First, Outside, Inside, and Last, referring to the order of multiplying terms. You multiply first terms, then outside terms, then inside terms, then last terms, and then combine like terms for your answer.
STEP 2: Write the given problem
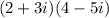
STEP 3: Use the FOIL method to multiply the problem
![\begin{gathered} \mleft(2+3i\mright)\mleft(4-5i\mright) \\ \text{FOIL method states that:} \\ \mleft(a+b\mright)\mleft(c+d\mright)=ac+ad+bc+bd \\ \text{Comparing with the given problem,} \\ a=2,\: b=3i,\: c=4,\: d=-5i \\ =(2*\: 4)+2\mleft(-5i\mright)+(3i*4)+(3i*\mleft(-5i\mright)) \\ To\text{ open the bracket, apply the minus-plus rules} \\ +\mleft(-a\mright)=-a \\ The\text{ new solution becomes:} \\ =(2*\: 4)-(2*\: 5i)+(3*\: 4i)-(3i*\: 5i) \\ =8-10i+12i-15ii \\ =8-10i+12i-15i^2 \\ \text{ Using the square rule of imaginary numbers} \\ i^2=-1 \\ By\text{ substitution,} \\ =8-10i+12i-15(-1) \\ =8-10i+12i+15 \\ \text{Collecting like terms;} \\ =23+2i \end{gathered}]()
Hence, the breakdown of the FOIL method for the problem is:
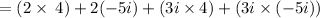
The answer to the question becomes:
Using the FOIL method, the product of the first terms is 8, the product of the outside terms is -10i and the product of the inside terms is 12i. The product of the last terms in terms of i² is -15i², which simplifies to 23+2i