Question

what is the horizontal distance from which the archerfish can hit the Beatle? how much time does the beetle have to react in this case?

Answer 1

The given problem can be represented using the following diagram:

We will use the non-parametric equation for the projectile motion:

`y=y_0+x\tan \theta-(gx^2)/(2v^2_0\cos^2\theta)`

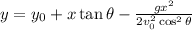
Where:

`\begin{gathered} y=\text{ vertical reach} \\ y_0=\text{ initial height} \\ x=\text{ horizontal reach} \\ \theta=\text{ initial angle} \\ g=\text{ acceleration of gravity} \\ v_0=\text{ initial velocity} \end{gathered}`

Since the initial height is zero, we have:

`y=x\tan \theta-(gx^2)/(2v^2_0\cos^2\theta)`

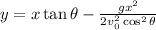
Now, we substitute the known values:

`y=x\tan (54)-(9.8x^2)/(2(2.6)^2(\cos ^2(54)))`

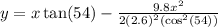
Simplifying we get:

`y=1.38x-2.1x^2`

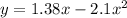
Now, we need to determine the value of "x" for which the value of "y" is 2.7 cm or in meters 0.027m. Substituting we get:

`0.027=1.38x-2.1x^2`

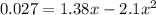
Now, we bring the terms on the right side to the left side by changing their signs:

`2.1x^2-1.38x+0.027=0`

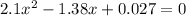
Now, we divide both sides by 2.1:

`x^2-0.66x+0.013=0`

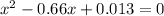
we get an equation of the form:

`ax^2+bx+c=0`

the solution is given by the quadratic formula as follows:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Substituting the values we get:

`x=\frac{-(-0.66)\pm\sqrt[]{(-0.66)^2-4(0.013)}}{2}`

solving the operations inside the radical we get:

`x=\frac{-(-0.66)\pm\sqrt[]{(0.38)}}{2}`

Now, we solve for the positive value:

`x=\frac{-(-0.66)+\sqrt[]{(0.38)}}{2}`

Solving the operations:

`x=0.64`

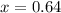
Now, we solve for the negative value:

`x=\frac{-(-0.66)-\sqrt[]{(0.38)}}{2}`

Solving the operations:

`x=0.02`

From the two possible values we take the smaller value, therefore, the horizontal reach is:

`x=0.02\text{meters. }`

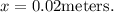
Or its equivalent 2 cm.

Part B. To determine the time we will use the following equation of motion for the projectile motion:

`x=(v_0\cos \theta)t`

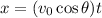
Now, we solve for "t":

`(x)/(v_0\cos \theta)=t`

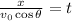
Now, we substitute the values:

`(0.02)/((2.6)(\cos 54))=t`

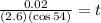
Solving the operations:

`0.013=t`

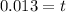
Therefore, the time is 0.013 seconds.