If the speed of the second train is represented by x, then the first train's speed is: x + 9.6
Then, we can form the following equation:
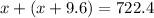
Next, solve for x:

This is the speed of the second train, and
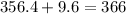
This is the speed of the first train
Answer:
the speed of the first train: 366 mph
the speed of the second train: 356.4 mph