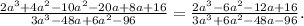Question

Only the circled questions I'm bad at math thank you

Answer 1

We have the following expression:

`(a^2-5a+4)/(3a+6)\cdot(2a+4)/(a^2-16)\text{.}`

In order to do the multiplication, we simply multiply the denominators and put the result in the denominator, and we multiply the denominators and put then in the denominator:

`((a^2-5a+4)(2a+4))/((3a+6)(a^2-16))\text{.}`

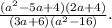
Before we continue, we need to determine the values of the variables for which the expression is not defined. Since we have a division, this will only happen if the denominator is equal to 0.

Since we have a multiplication in the denominator, the only way it will be 0 is if either of the factors is 0. In other words, we can't have

`3a+6=0,`

or

`a^2-16=0.`

For the first equation, we simply subtract 6 from both sides and hen divide by 3 to obtain

`a=-(6)/(3)=-2,`

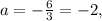
so a cannot be -2.

For the second equation, we can actually factor is further like this:

`a^2-16=(a+4)(a-4),`

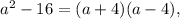
and from this we can see that it will be 0 if a is either 4 o -4. In other words, and putting all of this together, a cannot be -2, -4 or 4.

With that out of the way, let's proceed with the multiplication:

`((a^2-5a+4)(2a+4))/((3a+6)(a^2-16))=(2a^3+4a^2-10a^2-20a+8a+16)/(3a^3-48a+6a^2-96)\text{.}`

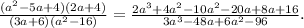
Grouping similar terms together gives us:

`(2a^3+4a^2-10a^2-20a+8a+16)/(3a^3-48a+6a^2-96)=(2a^3-6a^2-12a+16)/(3a^3+6a^2-48a-96)\text{.}`