We want to find the solution of the following inequality
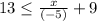
To find the solution for this inequality, we can start by multiplying both sides by (-5).
When we multiply an inequality by a negative number, the "side" of the sign changes
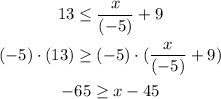
And finally, we can add 45 to both sides of the equation to get our solution.
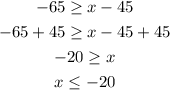
This is our final answer.
