SOLUTION
Define a variable for the unknown numbers.
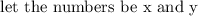
The sum is 23, implies
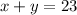
The difference is 9 is written as
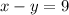
Then we have the system of equation
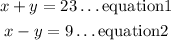
Add equation 1 and 2.
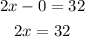
Divide both sides by 2
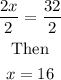
hence x=16
Recall equation 1
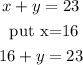
Subtract 16 from both sides, we have
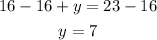
Hence, y=7
Answer: The numbers are 16 and 7