Given the line parallel to the required equation of a line ase are asked tof
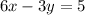
and the point the required line passes through as
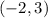
We can find the equation of the line parallel to 6x-3y=5 and passes through the point (-2,3) below:
Step-by-step explanation
First, we get the slope of the given line
The general equation of a line(slope -intercept form) is given as
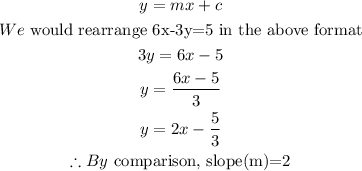
Since the line given in the questions is parallel to the required line, therefore,
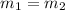
This implies their slopes are the same.
Next, we can apply all the derived parameters into the point-slope formula for the equation of a line and simplify to get the slope-intercept form
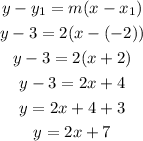
Therefore the required equation of the line is
Answer: y = 2x + 7