1 Answer

Cool Goose · Answer 1 · 2023-07-24T17:15:37+0000

We can find the volume of a sphere with the formula:

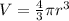
$V=(4)/(3)\pi r^3$

1) When the radius of the sphere is r=7 in, the volume V is:

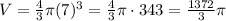
$V=(4)/(3)\pi(7)^3=(4)/(3)\pi\cdot343=(1372)/(3)\pi$

2) When the diameter of the sphere is d=33 in, the radius is r=33/2 and the volume V is:

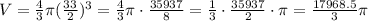
$V=(4)/(3)\pi((33)/(2))^3=(4)/(3)\pi\cdot(35937)/(8)=(1)/(3)\cdot(35937)/(2)\cdot\pi=(17968.5)/(3)\pi$

3) The surface area of a sphere can be calculated with the formula:

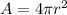
$A=4\pi r^2$

Then, if the sphere has a radius r = 2.8 in, the area A is:

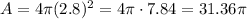
$A=4\pi(2.8)^2=4\pi\cdot7.84=31.36\pi$

4) In this case we know that the diameter is D = 24 mm, so the radius is r = 12 mm.

Then, the area is:

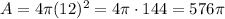
$A=4\pi(12)^2=4\pi\cdot144=576\pi$

Answer:

1) (1372/3) π

2) (17968.5/3) π

3) 31.36π

4) 576π

Please log in or register to add a comment.