Given,
The distance of the point source is decreased by a factor of 3 times.
That is,
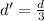
Where d' is the new distance and the d is the old distance.
(a)
The intensity is given by,
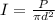
Where P is the power.
Thus the intensity after the distance is decreased is,
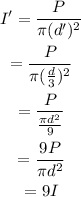
Therefore, the intensity is increased by a multiplicative factor of 9.
(b)
The intensity level when the distance is d is given by,

The intensity level when the distance id d' is given by,
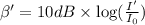
On substituting I'=9I in the above equation,
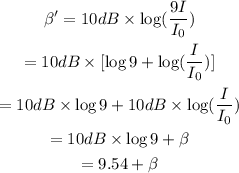
Thus the intensity level increase by an additive amount of 9.54