1 Answer

StinkySocks · Answer 1 · 2023-11-03T03:10:50+0000

Question:

Solution:

Let the following linear function:

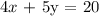
$4x\text{ + 5y = 20}$

solve for 5y:

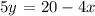
$5y\text{ = }20-4x$

solving for y, we get:

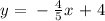
$y\text{ = }-(4)/(5)x\text{ + }4$

the y- intercept is when x = 0, then replacing x = 0 into previous equation we get:

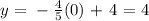
$y\text{ = }-(4)/(5)(0)\text{ + }4\text{ = 4}$

then the y-intercept is the point:

(x,y) = (0,4)

Now, the x-intercept is when y = 0, the replacing y = 0 into the equation:

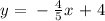
$y\text{ = }-(4)/(5)x\text{ + }4$

we get:

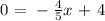
$0\text{ = }-(4)/(5)x\text{ + }4$

this is equivalent to:

$-4\text{= }-(4)/(5)x\text{ }$

this is equivalent to:

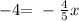
$4\text{= }(4)/(5)x\text{ }$

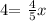
solving for x, we get:

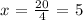
$x\text{ = }(20)/(4)\text{ = 5}$

then the x-intercept is the point:

(x,y) = (5,0)

Then, we can conclude that the correct answer is:

1. the y-intercept is the point (x,y) = (0,4).

2. the x-intercept is the point (x,y) = (5,0).

and the graph of the line is:

Please log in or register to add a comment.