Question

Need help with number 5. Verify the holes, vertical asymptotes, and horizontal asymptotes of each. Then sketch the graph

Answer 1

Function given:

`f\mleft(x\mright)=(1)/(2x^2+2x-12)`

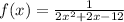
Procedure

• Finding the hole

Factor the polynomial in the denominator:

`f\mleft(x\mright)=(1)/(2(x^2+x-6))`
`f(x)=(1)/(2\lbrack(x+3)(x-2)\rbrack)`

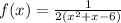
If there was a hole, there would have to be a common factor between numerator and denominator. Therefore, as this function has no common factor between numerator and denominator, then there is no hole for the rational function.

• Vertical asymptotes

In this case, we also have to factor the denominator. As we already did, we know that the factored expression is:

`f(x)=(1)/(2\lbrack(x+3)(x-2)\rbrack)`

Then, we have to equal those factors to 0, meaning:

`x+3=0`
`x-2=0`

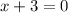
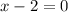
Solving for x, we get the vertical asymptotes:

`x=-3`
`x=2`

Then, the vertical asymtotes are x = -3 and x = 2.

• Horizontal asymptotes

In this case, we have to calculate the limits of the function:

`\lim _(x\to\infty)((1)/(2x^2+2x-12))`
`\lim _(x\to-\infty)((1)/(2x^2+2x-12))`

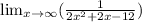
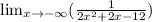
Solving the limits we get:

`(1)/(2\infty^2+2\infty-12)=(1)/(\infty)=0`
`(1)/(2(-\infty)^2+2(-\infty)-12)=(1)/(\infty)=0`

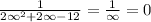
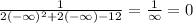
Then, the horizontal asymptote is y = 0.

Answer:

• Holes: None.

,

• Vertical asymptotes: ,x = -3 ,and ,x = 2,.

,

• Horizontal asymptotes: ,y = 0.

• Graph